[最も共有された! √] 四��形 内角の和 証明 114544-四���形 内角の和 証明
赤線の補助線を入れると四角形の内角の和から \(\hspace{10pt}360()\\ =\\ =\color{red}{118} (度)\) この\(\,\color{red}{118°}\,\)は右下の三角形の1つの外角なので\(\,∠x\,\)の補角は \(\hspace{10pt}118^{\circ}38^{\circ}\\ =\color{blue}{80^{\circ}}\) よって \(\begin{eqnarray}
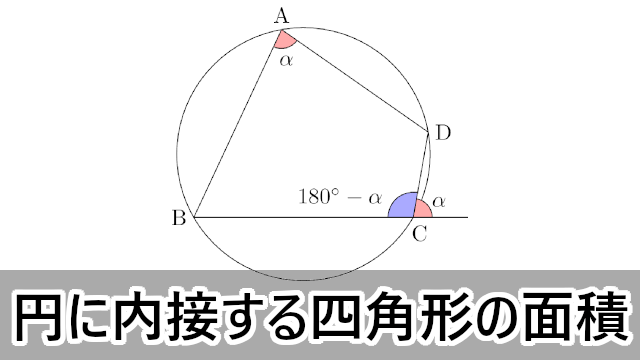
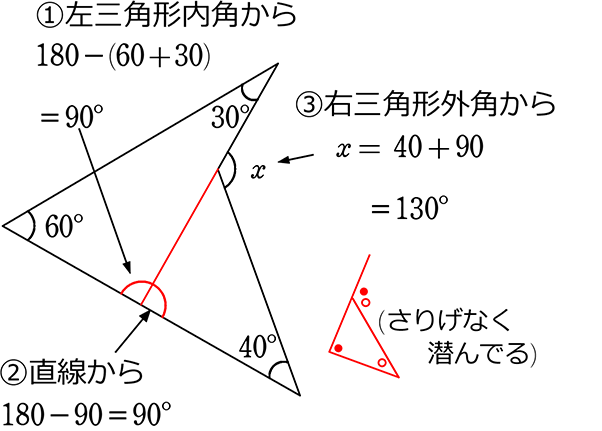
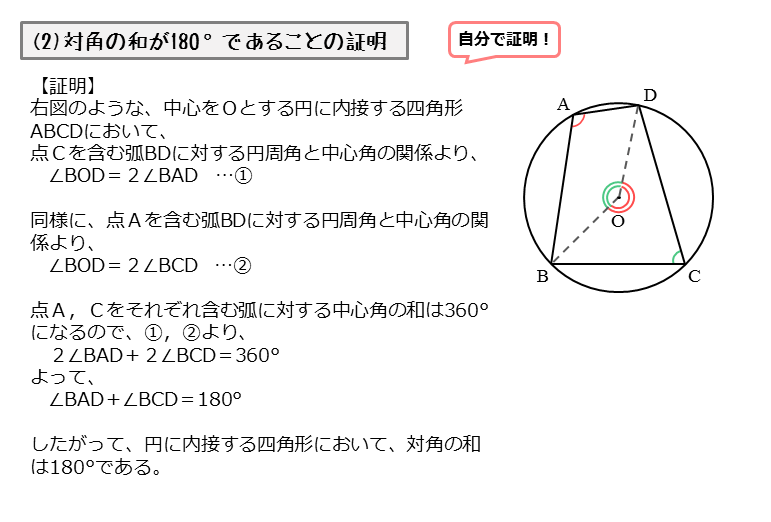
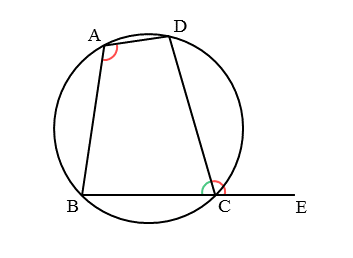
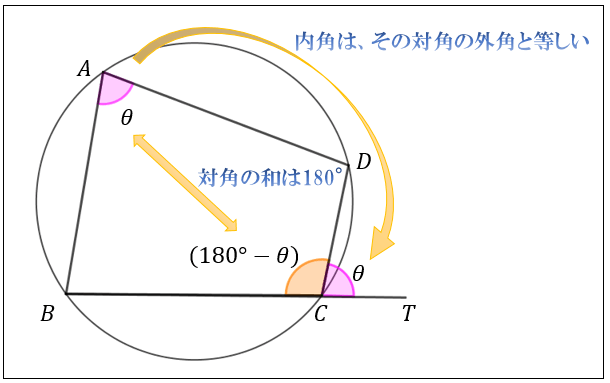
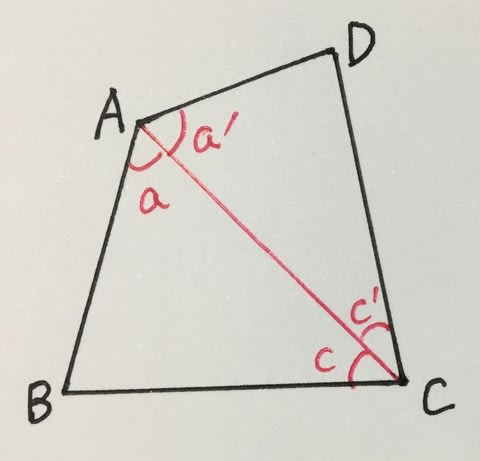
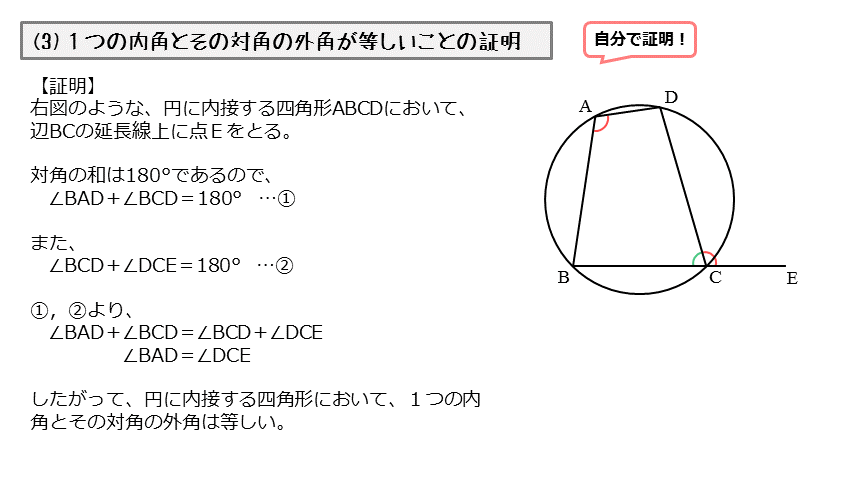
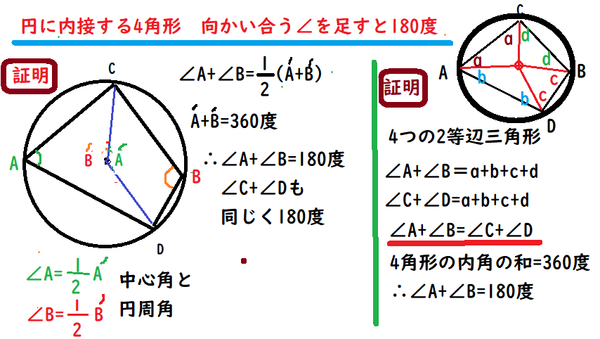
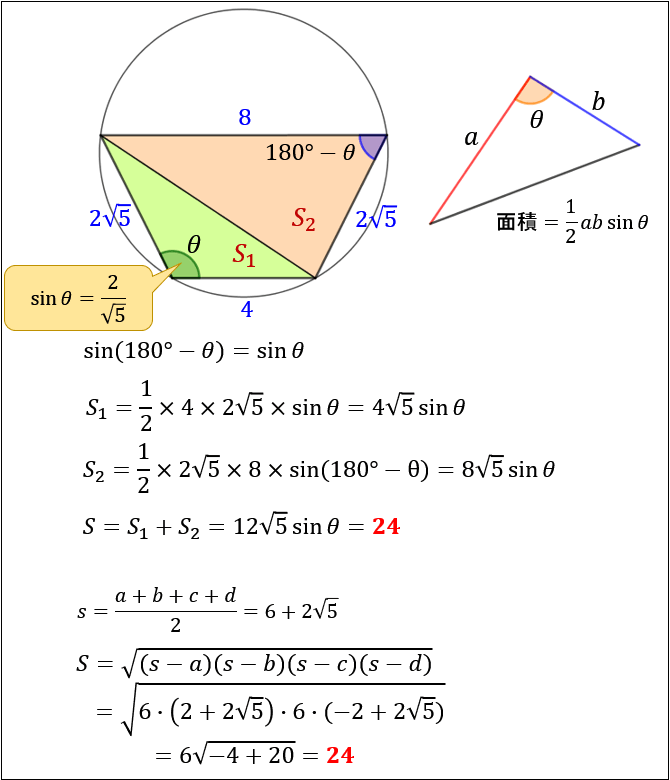
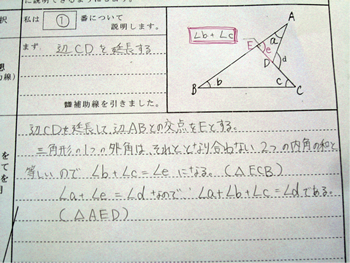
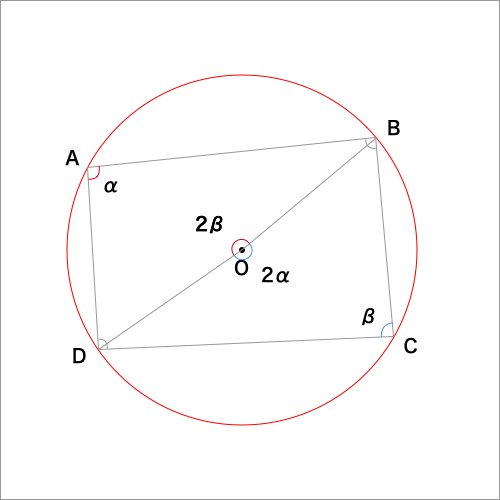
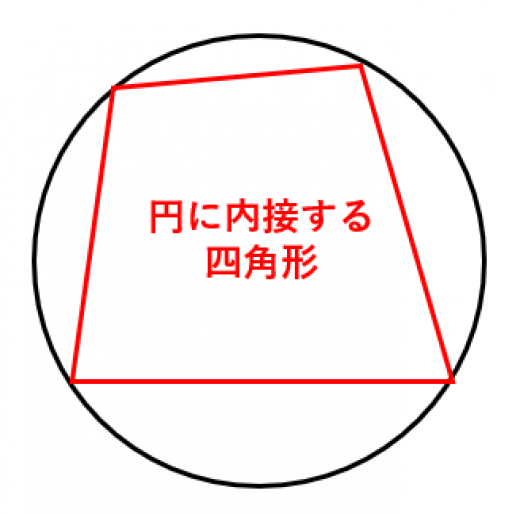
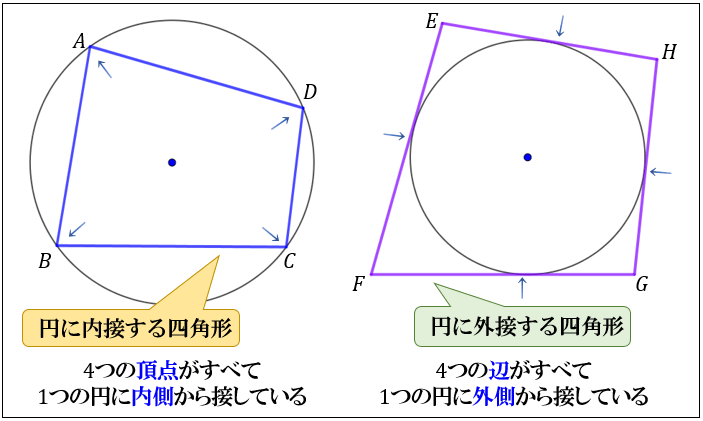
四角形 内角の和 証明- ③錯角より、∠abd=∠bae ∠adb=∠daf ∠bae∠bad∠daf=180° よって、 abdの内角の和は180° 同じようにして、 bcdの内角の和も180° ④四角形abcdの内角の和= abdの内角の和 bcd の内角の和なので 180°180°=360° したがって 四角形の内角の和は360° どうでしょうか。 ① 対角の和は180° ② トレミーの定理 ③ 方べきの定理 ④ ブラーマグプタの公式 ① 対角の和は180° 円に内接する四角形の対角の和は 180 ° 円に内接する四角形の内角は、その対角の外角と等しい まず、円に内接する四角形では ∠ A ∠ C = 180 ° が成り立ちます。 対角の和が 180 ° になる理由は、 円周角の定理 から説明できます。 円の中心を点 O 、 ∠ A = θ とおくと 円周角の定理 より
四角形 内角の和 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
 |  |  |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
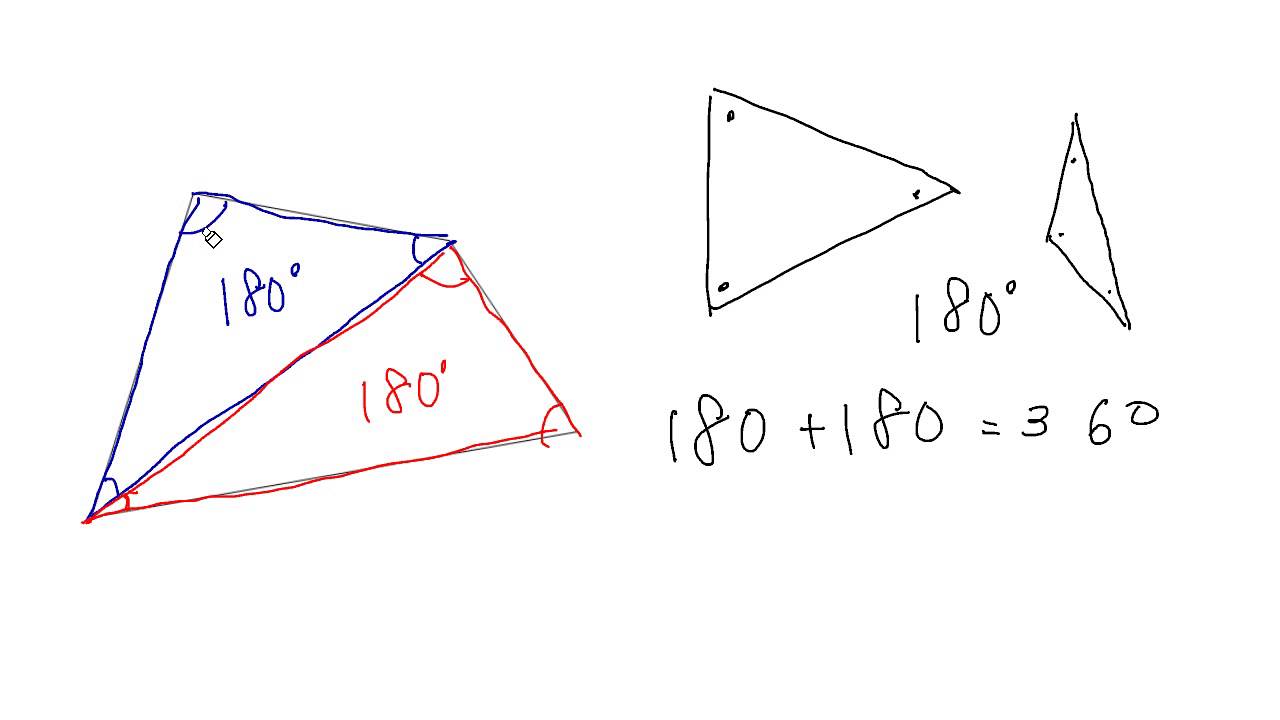 |  | |
 |  |  |
 | ||
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「四角形 内角の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 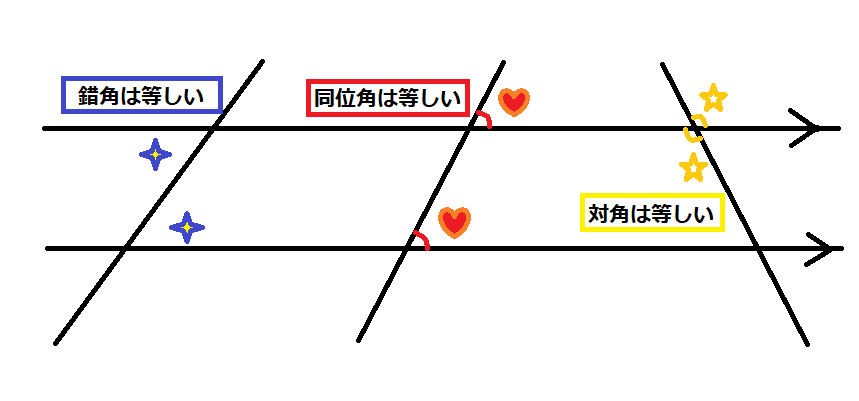 |
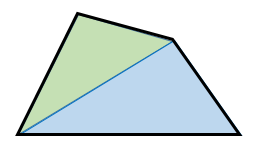
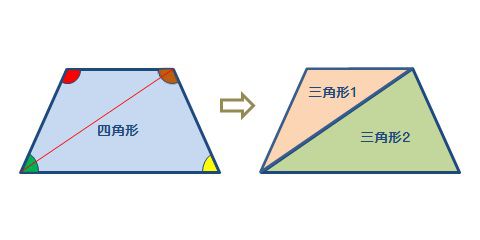
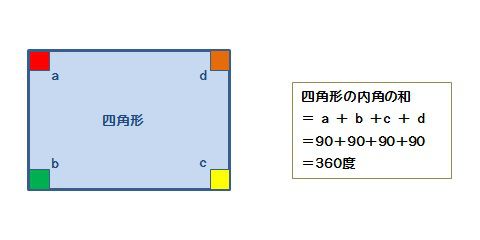
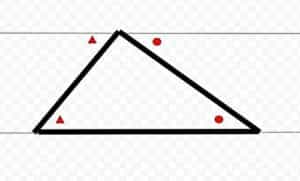
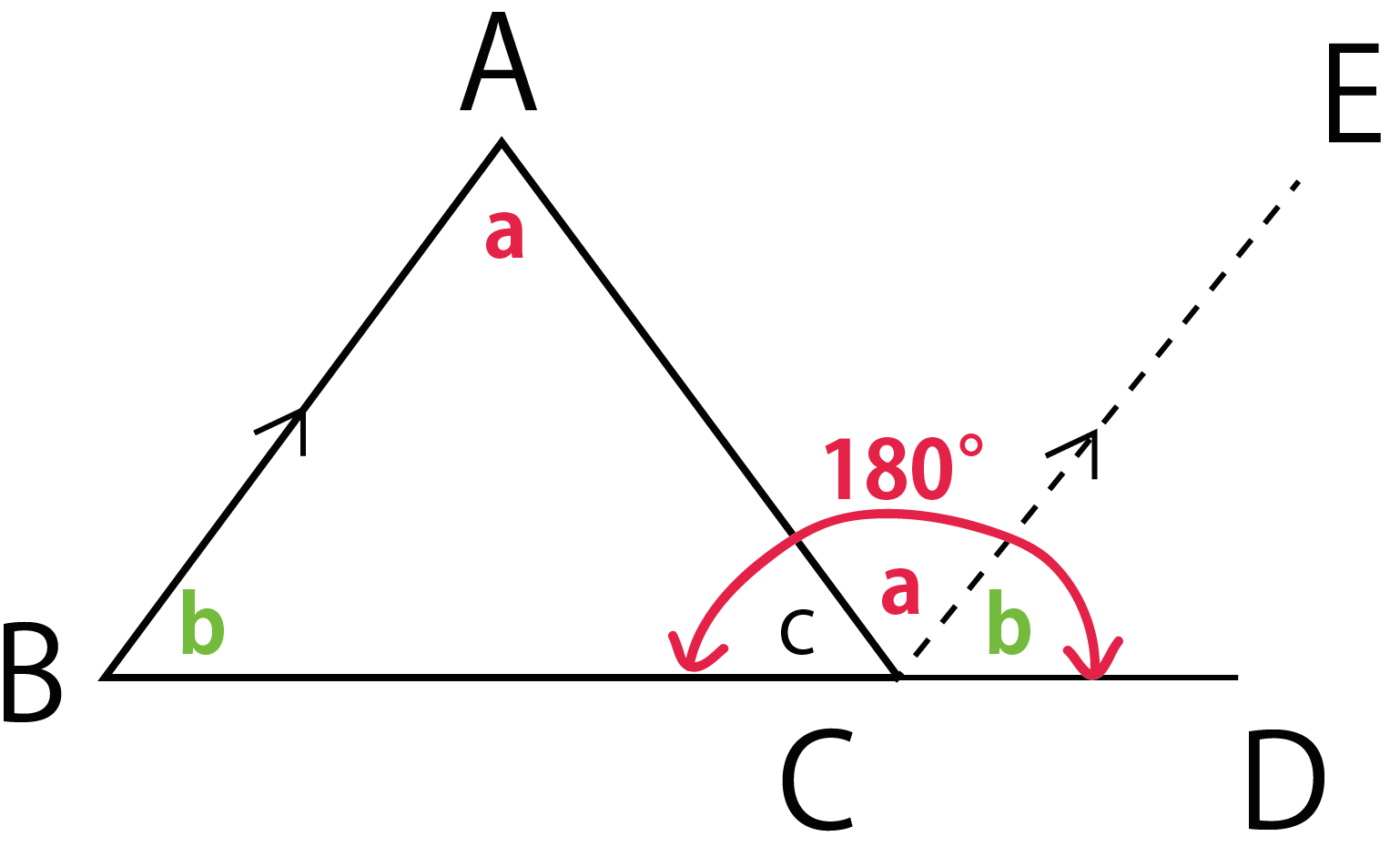
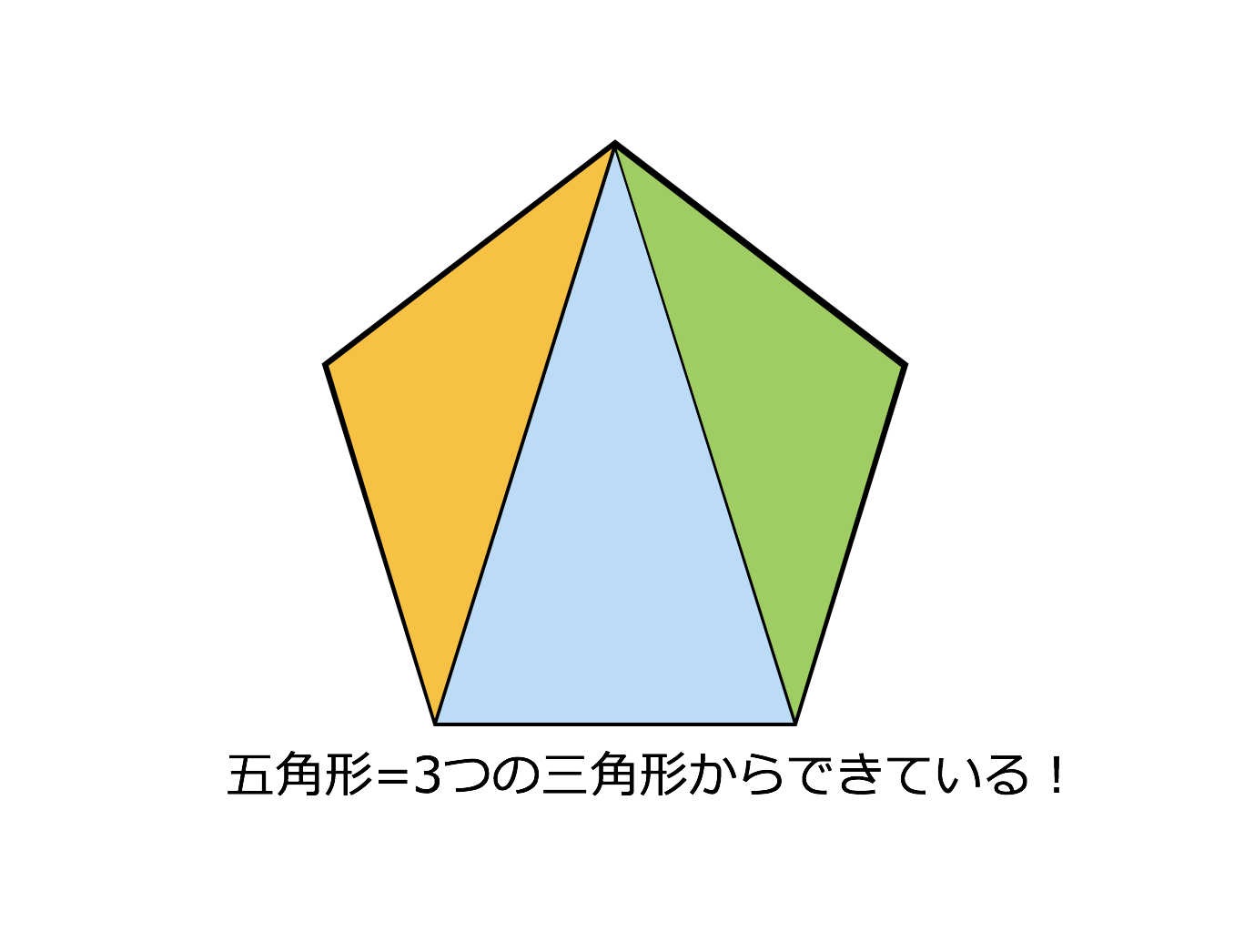
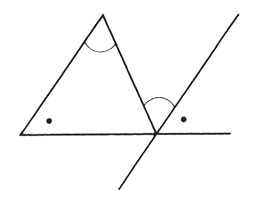
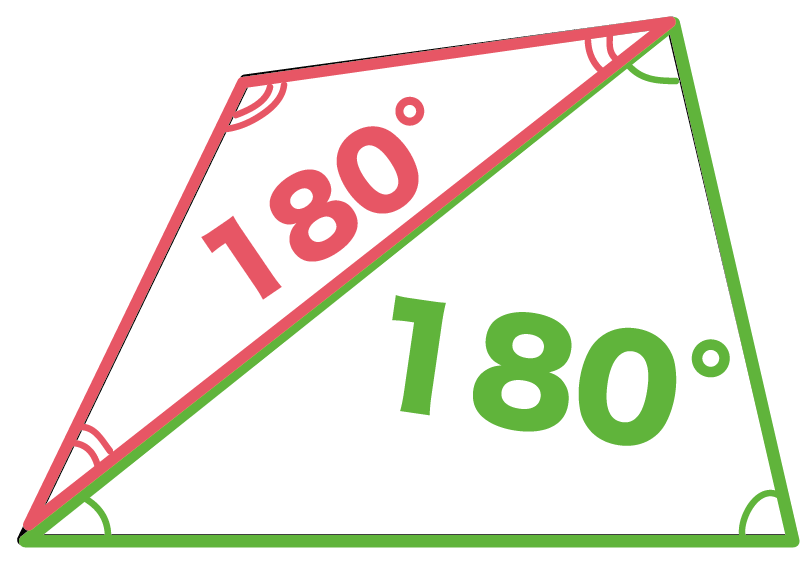
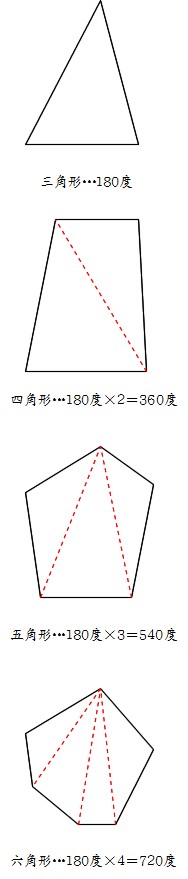
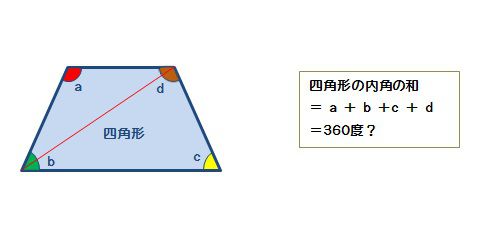
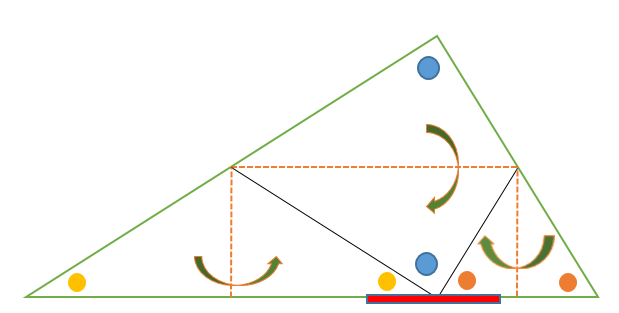
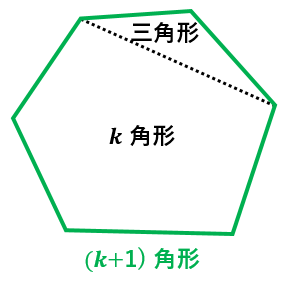
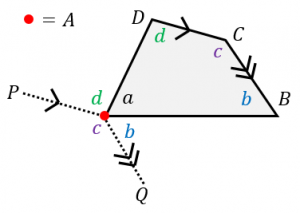
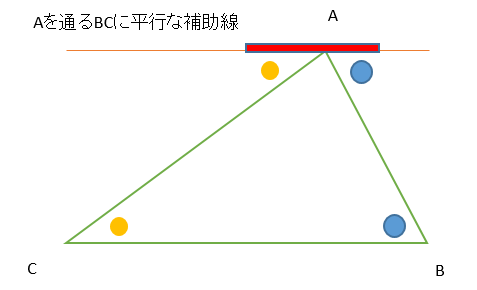
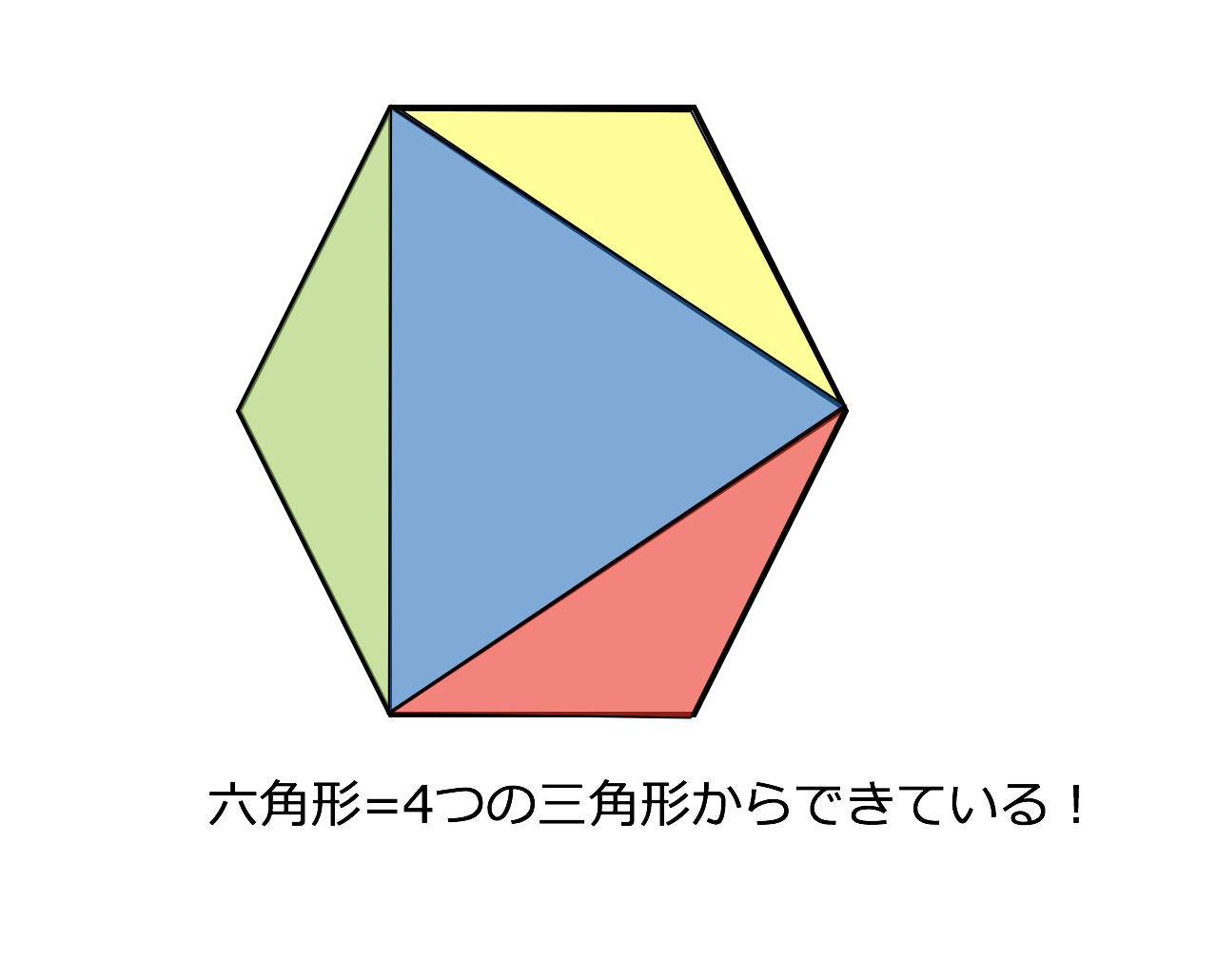
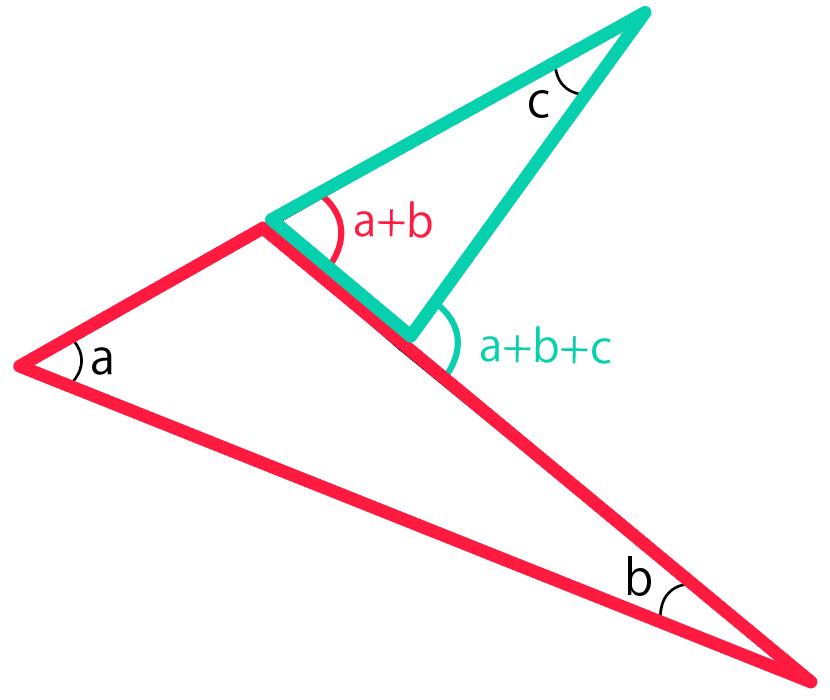
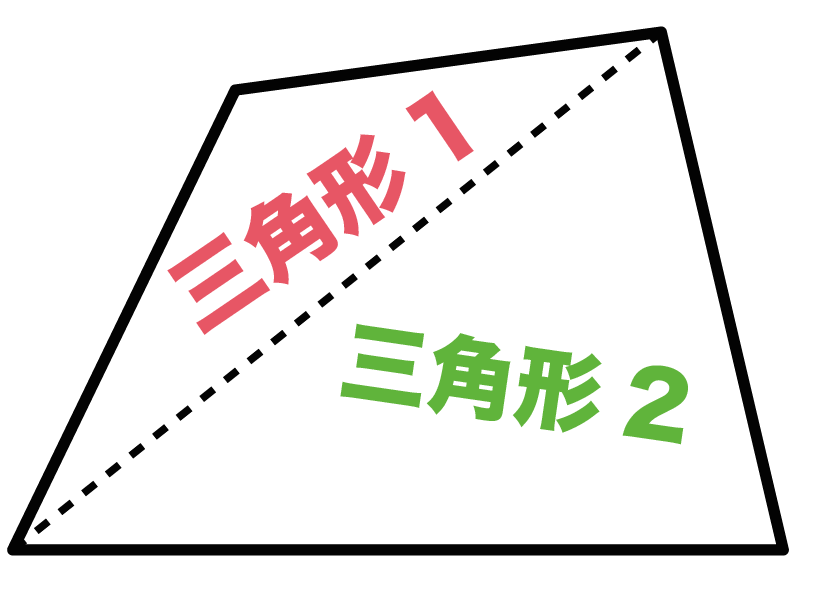
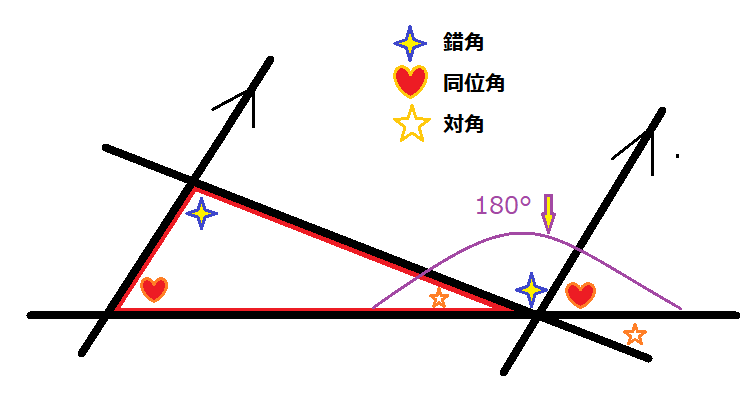
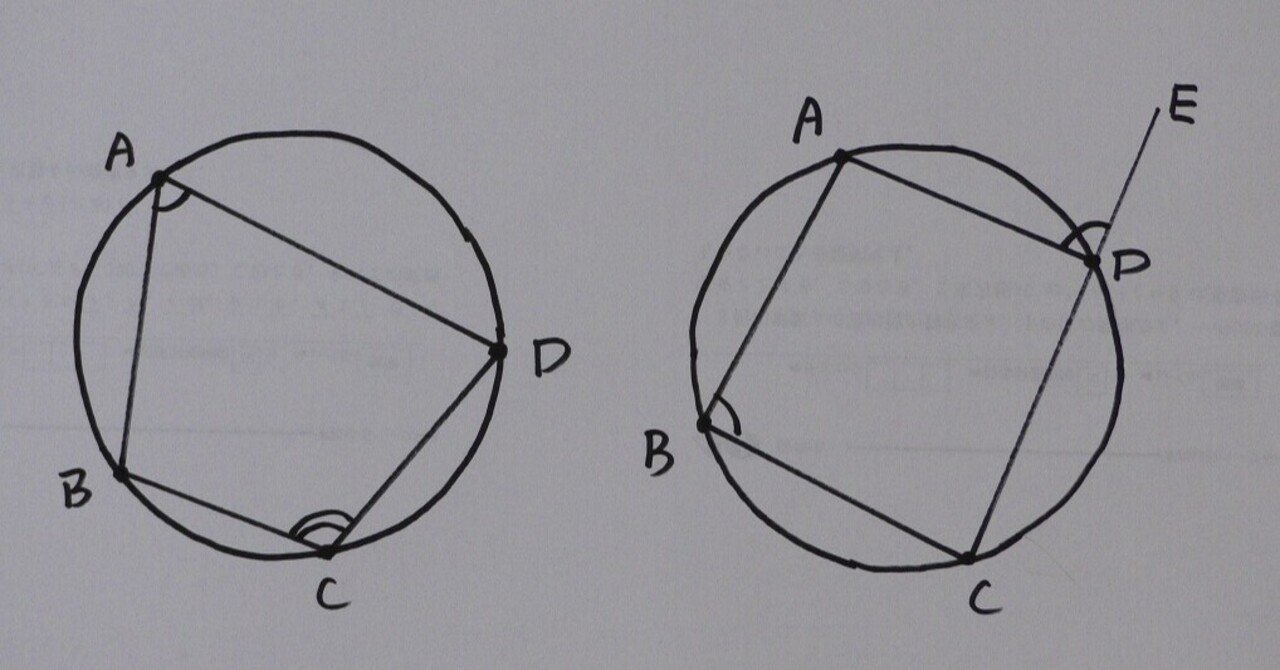
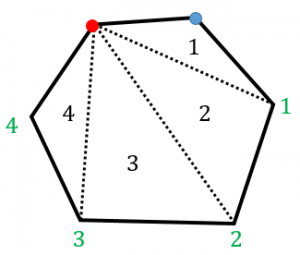
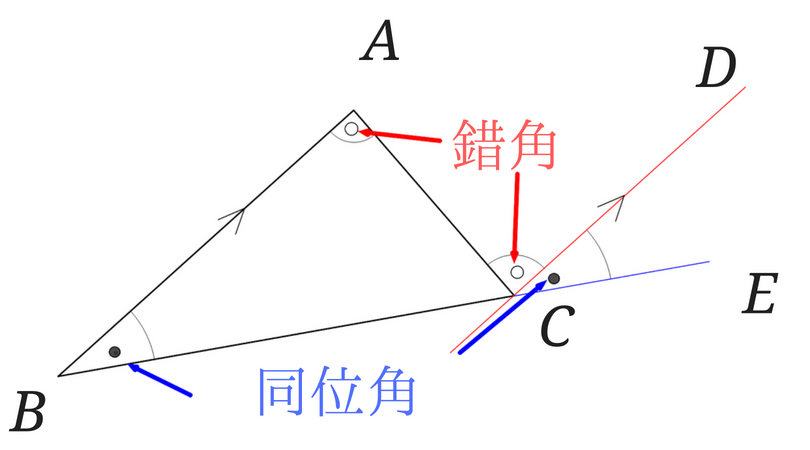
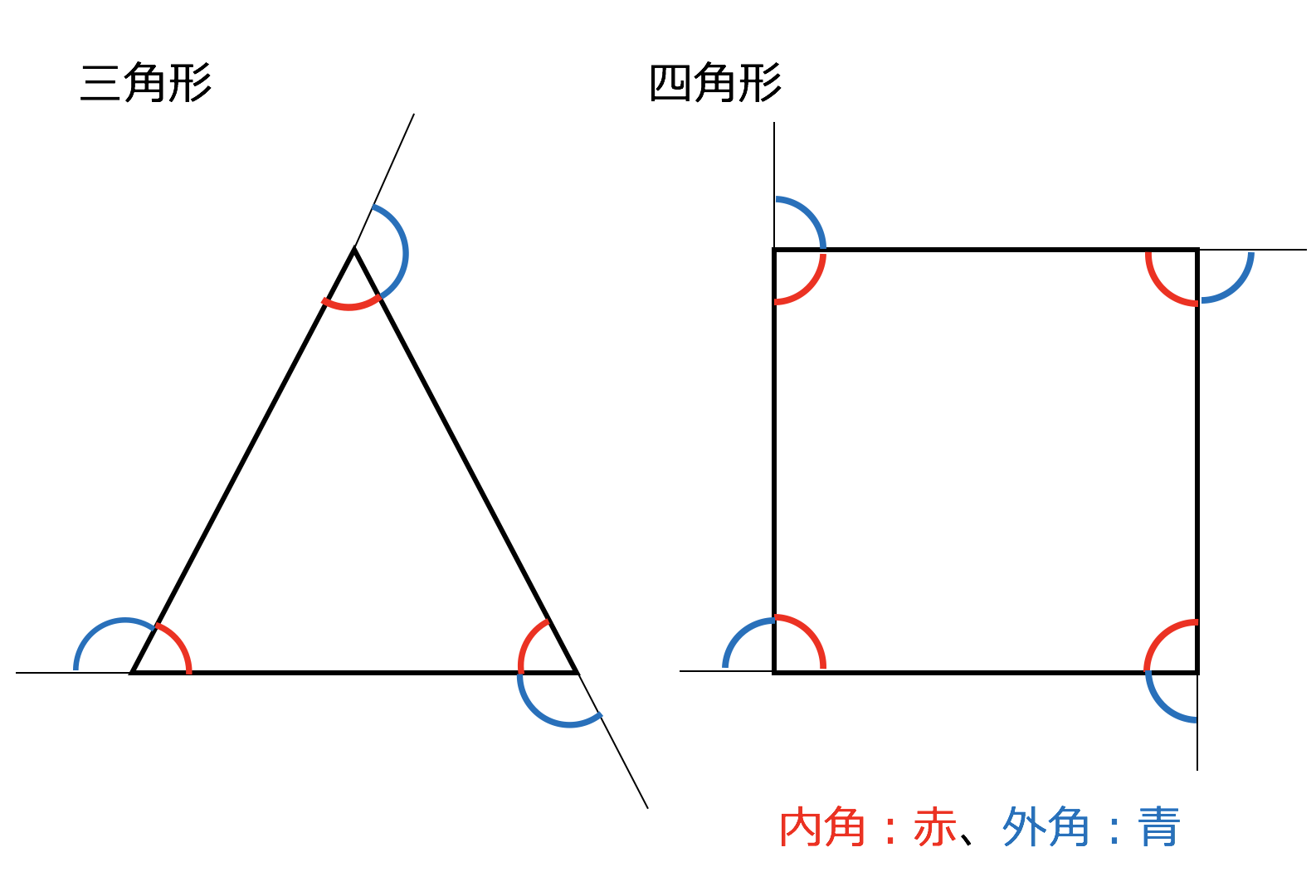
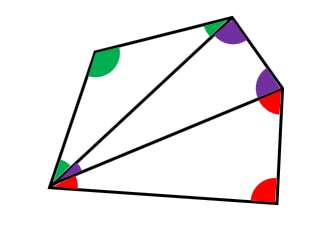
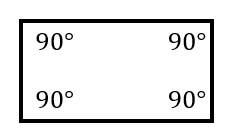
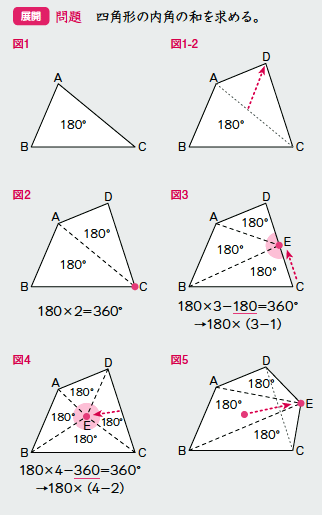
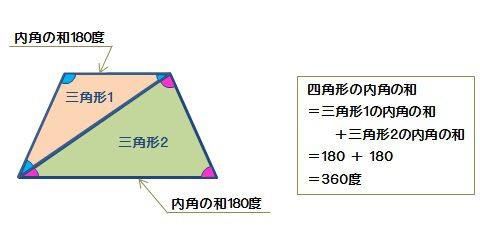
四角形の内角の和がいくつになるのか忘れてしまったら、長方形や正方形を使って思い出しましょう。 この記事の残りでは、四角形の内角の和が360°であることを2通りの方法で証明します。 証明1 四角形に対角線を一本引いて、三角形2つに分けます。 小学校の教科書にはこちらの方法が載っています。 三角形の内角の和が 180 ∘ である という性質を使います。 すると、 青い三角形の内角の和 は内角の和が180°になる証明 まず証明の簡単な概要について説明します。 図のように三角形の1辺を延長し、さらに1辺と平行な線を引きます。 平行線の錯角・同位角が等しいことから、三角形の内角と等しい角度が外角にできます。 内角の和と等しい角度が1直線に並ぶため180°と等しいことがわかりました。 以上をきちんと証明するには以下のようになります
Incoming Term: 四角形 内角の和 証明,
コメント
コメントを投稿